Bilan logico-mathématique ou comprendre les difficultés en math

Je vous propose en introduction une conférence que j’avais donné il y a quelques années, attention il vous faut 1h15 devant vous 🙂

1. le bilan logio-mathématique

Plusieurs outils sont à la disposition des professionnels, j’ai choisi d’utiliser le Tedi-Math et le Tedi-Math Grands qui offrent la possibilité de tester les enfants de la Moyenne Section de Maternelle à la 5ème. Il permet d’évaluer :

• l’acquisition de la chaîne numérique verbale
• le dénombrement
• les stratégies de calcul en arithmétique

Les difficultés logico-mathématiques apparaissent rarement seules. Dans 40% des cas, les enfants soumis à une difficulté d’ordre « dys » en présente généralement plusieurs. Aussi avant de faire le bilan logico-mathématique il est important de connaitre le cadre dans lequel on se trouve : d’autres bilans ont-ils été faits? Auprès de qui?…

Un bilan se pense donc en 3 temps :

1. 1h de rencontre d’anamnèse : vous venez avec votre enfant et nous prenons le temps de faire connaissance mais aussi d’étudier les différents bilans déjà réalisés, les cahiers de votre enfant, ses évaluations et notamment la nature de ses erreurs, ses bulletins de note.
2. le moment du bilan proprement dit, 2 possibilités dans ce cadre :
   • soit un bilan psychométrique a déjà été réalisé et/ou un bilan orthophonique de langage et/ou un bilan psychomoteur et/ou une rencontre avec un neuropédiatre posant des diagnostics; dans ce cadre nous ne réalisons que le bilan logico-mathématique, les autres difficultés de votre enfant étant déjà connues par ailleurs (prévoir 2h de bilan)
   • soit aucun bilan d’aucune sorte n’a jamais été réalisé auquel, la réalisation d’un bilan psychométrique en plus du bilan logico-mathématique est fortement conseillé. En effet, cela permettra de mieux comprendre le contexte dans lequel les difficultés logico-mathématiques apparaissent et ainsi de pouvoir proposer des aides plus adaptées. En effet, si les difficultés logico-mathématiques s’inscrivent par exemple dans un contexte de difficultés visuo-spatiales, il est important de le déterminer. Le bilan psychométrique permet de tester en une passation des compétences de langage, d’organisation visuo-spatiale et visuo-constructives, de raisonnement inductif, quantitatif ainsi que des capacités plus fonctionnelles telles que la mémoire de travail ou la vitesse de traitement. Je vous laisse lire le paragraphe 2 pour mieux comprendre les éventuels liens entre ces différentes compétences et une dyscalculie. (prévoir 2 fois 2h de bilan)
   • A la suite de ces bilans, il me faut entre 2 et 4h de travail comprenant : analyse, cotation, dépouillement éventuel de questionnaires, mise en relation avec les autres professionnels gravitant autour de votre enfant
3. 1h de restitution : nous prévoyons une dernière rencontre dans laquelle je vous explique les résultats obtenus ainsi que les éventuelles aménagements qui pourraient être mis en place au quotidien

TARIF : j’applique un tarif horaire à 55€, le bilan logico-mathématique représente donc :

• seul : 6h de travail (4h de rencontre et 2h de travail sur le dossier) pour une facture totale à 330€
• avec un bilan psychométrique : 10h de travail (6h de rencontre et 4h d’analyse) pour une facture totale à 495€

Des facilités de paiement sont bien évidemment possible. Les bilans ne sont pas pris en charge par la sécurité sociale, les mutuelles peuvent parfois y participer selon votre contrat.

2. Pourquoi un tel bilan ?

DSM V : Trouble spécifique des apprentissages
Difficultés à apprendre et à utiliser des compétences scolaires ou universitaires, les symptômes doivent persister pendant plus de 6 mois malgré la mise en place de mesures ciblant ces difficultés. Ces difficultés apparaissent chez des enfants d’intelligence normale (sans déficience intellectuelle) qui ne présentent pas de déficit neurologique ou sensoriel.
Concernant le calcul, il est également possible de parler de dyscalculie. Ce terme décrit un ensemble de problèmes caractérisés par des difficultés à :

• traiter des données numériques
• apprendre des faits arithmétiques
• réaliser des calculs exacts et fluides

Des difficultés connexes peuvent venir compléter celles déjà citées telles que des difficultés de raisonnement mathématique ou de raisonnement verbal.

La dyscalculie se manifeste généralement à l’âge scolaire avec l’apprentissage des mathématiques. Elle concerne comme la dyslexie entre 3,5 et 8% des enfants selon les critères de mesure employés dans les études.

Il est très rare qu’un trouble des apprentissages soit isolé. Dans près de 40% des cas, un enfant concerné par un trouble des apprentissages (dyslexie, dyspraxie, dysorthographie, dyscalculie, dysphasie…) en présente plusieurs. Le trouble spécifique des apprentissages avec déficit du calcul est souvent combiné à un trouble du langage ou à un trouble développemental de la coordination (anciennement nommé dyspraxie).

3. Quelques mots sur le développement précoce du nombre

Pour un développement plus complet du sujet, je vous propose une vidéo captée lors d’un séminaire sur le développement des compétences numérique d’où est également tiré la vidéo précédente :

La capacité à discriminer les quantités est une compétence que l’on retrouve aussi bien chez le bébé mais aussi chez l’animal comme les singes, les rats ou les pigeons (pour une synthèse, Brannon, 2005).

Les nouveau-nés (moins de 12 mois) semblent également en mesure de traiter les quantités. Pour cela, ils mobiliseraient deux systèmes différents pour le traitement des quantités. L’un, précis mais ne s’appliquant qu’ à de petits ensembles allant de 1 à 3 éléments et ; l’autre, extensible aux très grandes quantités, fournissant
une évaluation approximative suivant la loi de Weber (Fayol et Seron, 2005). Les chercheurs n’ont jusqu’ici par encore tranché la question du caractère spécifiquement numérique de ces modes de
traitement tout comme celle des caractéristiques des représentations sur lesquelles ils pourraient s’effectuer.

Les premiers apprentissages numériques font appel au langage et suivent une certaine chronologie :

• acquisition de la chaîne verbale entre deux et six ans. Fuson et coll. (1982) ont établi que les suites numériques produites par les enfants en cours d’apprentissage s’organisent initialement suivant trois parties :
  

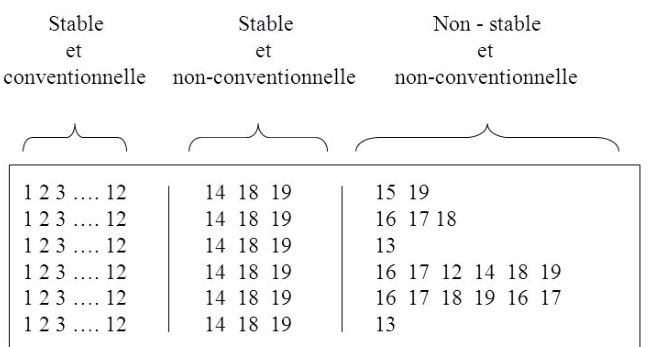
La partie stable et conventionnelle s’accroît avec l’âge, la partie stable et non conventionnelle concerne surtout les nombres de 10 à 19, enfin la partie ni stable ni conventionnelle change d’un essai à l’autre et peut également contenir des mots nombres inventés. D’un apprentissage initialement par cœur d’une comptine numérique, les enfants vont peu à peu grâce à la maîtrise de la combinatoire autour de 4ans 1/2 développer leurs connaissances. La différence entre les enfants ayant acquis la combinatoire et ceux utilisant du par coeur est d’autant plus manifeste dans les pays occidentaux présentant des systèmes verbaux irréguliers (« quatre-vint-dix ») contrairement aux pays du sud-est asiatiques chez qui la base 10 est plus saillante (pour une synthèse, voir Fayol, 2002)

• Processus de quantification : 3 processus sont à distinguer :
  • le subitizing : processus perceptif rapide et sûr d’appréhension immédiate de la quantité pour les petites numérosités, c’est-à-dire inférieures à 3 ou 4 objets
  • le dénombrement : 2 écoles s’affrontent
    • Gelman et Gallistel (1978) estiment qu’il faut maitriser 5 principes :
      • le principe de correspondance un à un (chaque élément de la collection à dénombrer est associé à une seule étiquette) ;
      • le principe d’ordre stable (la suite des étiquettes constitue une liste ordonnée) ;
      • le principe de cardinalité (la dernière étiquette utilisée représente le cardinal de la collection)
      • le principe d’abstraction (l’hétérogénéité des éléments n’a pas d’impact sur leur dénombrement)
      • le principe de non-pertinence de l’ordre (l’ordre dans lequel les éléments sont dénombrés n’a pas d’incidence sur le cardinalité (la dernière étiquette utilisée représente le cardinal de la collection).
    • Fuson (1988) suppose elle, que les principes sont progressivement abstraits d’une pratique répétée des procédures de dénombrement acquises par imitation
  • l’estimation : capacité à estimer la numérosité d’une collection pouvant aller jusqu’à plusieurs centaines de points chez l’adulte entraîné
• l’émergence des outils arithmétiques : des expériences, dont les conclusions sont controversées (Wynn, 1992), mettraient en évidence des capacités très précoces d’opérations arithmétiques (additions et soustractions simples) chez des nourrissons. Ce qui fait en revanche consensus, c’est qu’à partir de 5 ans beaucoup d’enfants de diverses cultures résolvent des problèmes arithmétiques simples (ajouts et retraits de quantités correspondant à des nombres à 1 chiffre) à l’aide du comptage (Siegler et Jenkins, 1989).
  Dès 3 ans les enfants vont utiliser des stratégies de résolution de problèmes arithmétiques (quasiment identiques entre additions et soustractions). La littérature met en avant 5 classes générales de stratégies pour résoudre des opération simples telles que 5 + 2 :
  • l’utilisation d’objets (utilisée dés l’âge de 3 ans)
  • le comptage sur les doigts (La transition du comptage sur les doigts au comptage verbal est progressive et dépend principalement de la capacité de l’enfant à contrôler mentalement le déroulement du calcul et à conserver une trace de ce qui a déjà été et de ce qui reste à compter)
  • le comptage verbal,
  • les décompositions
  • la récupération directe en mémoire du résultat
    

Des liens utiles :

une publication trés complète de l’INSERM sur les difficultés d’apprentissage dont la dyscalculie (chapitre 4) https://www.ipubli.inserm.fr/handle/10608/73

la présentation d’une collègue, C. THEVENOT de l’université de Genève sur les outils de dépistage de la dyscalculie (et notamment le TEDI-MATH) https://slideplayer.fr/slide/1148605/